Взаимное расположение точки, прямых и плоскостей с примерами

Плоскость. Способы ее задания, положение относительно плоскостей проекций

Положение плоскости в пространстве может быть однозначно определено:

— тремя точками, не лежащими на одной прямой;
— прямой и точкой, не лежащей на этой прямой;
— двумя параллельными прямыми;
— двумя пересекающимися прямыми;
— плоской фигурой;
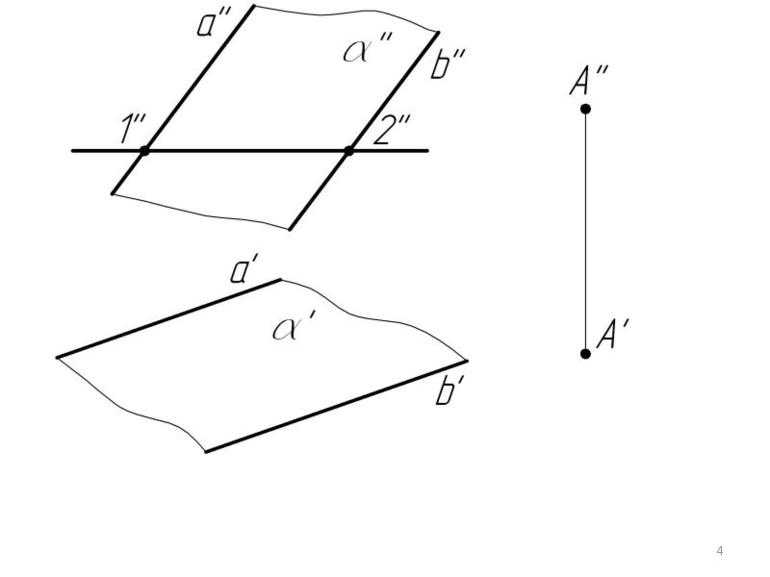
— следом плоскости.

Всегда от одного способа задания плоскостей можно перейти к другому.

След плоскости – это линия пересечения заданной плоскости с одной из плоскостей проекций.

Соответственно различают горизонтальный, фронтальный и профильный следы плоскости.

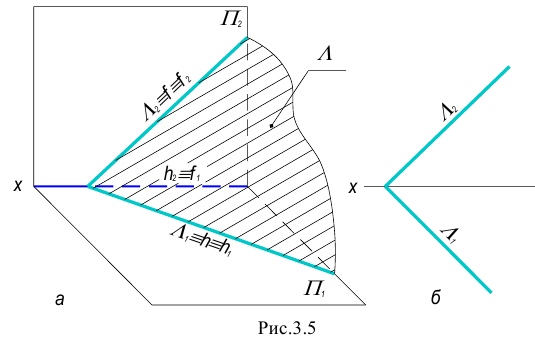
Плоскостью общего положения называется плоскость не параллельная и не перпендикулярная ни одной из плоскостей проекций.

Плоскостями частного положения относительно плоскостей проекций называются плоскости параллельные или перпендикулярные им.

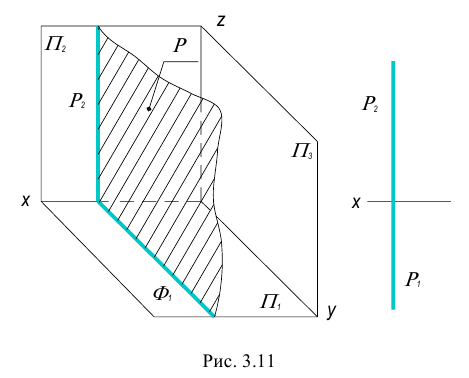
Плоскость перпендикулярная одной из плоскостей проекций называется проецирующей плоскостью.

Существует три вида проецирующих плоскостей: горизонтально- проецирующая, фронтально-проецирующая и профильно-проецирующая плоскости. Такие плоскости вырождаются в прямую линию (след плоскости) на ту плоскость проекций, к которой они перпендикулярны.

1. Горизонтально-проецирующая плоскость — плоскость перпендикулярная горизонтальной плоскости проекций.

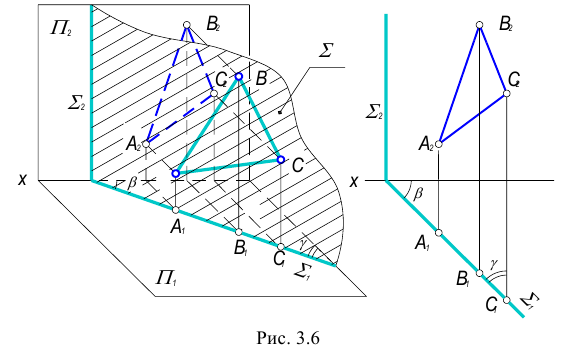
2. Фронтально-проецирующая плоскость – плоскость перпендикулярная фронтальной плоскости проекций.

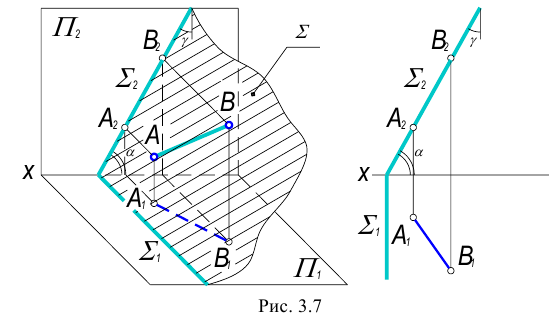
3. Профильно-проецирующая плоскость – плоскость, перпендикулярная профильной плоскости проекций.

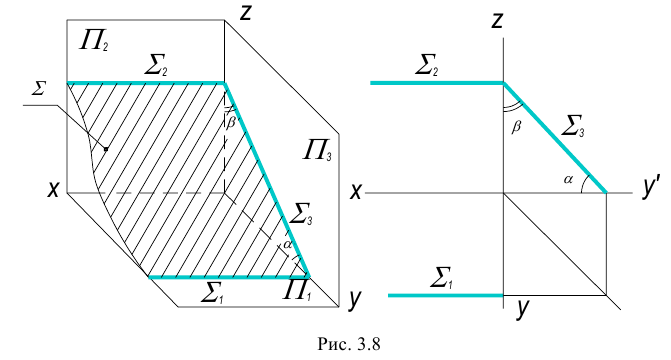
Плоскость, параллельная одной из плоскостей проекций, называется плоскостью уровня.

Существует три вида плоскостей уровня: горизонтальная, фронтальная и профильная плоскости уровня.

1. Горизонтальная плоскость – плоскость, параллельная горизонтальной плоскости проекций.

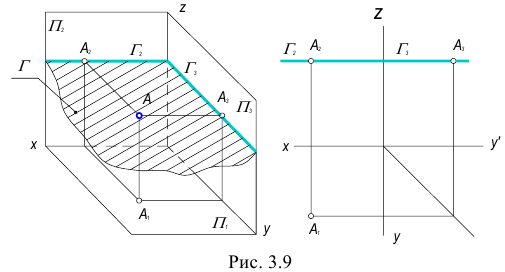
2. Фронтальная плоскость — плоскость, параллельная фронтальной плоскости проекций.

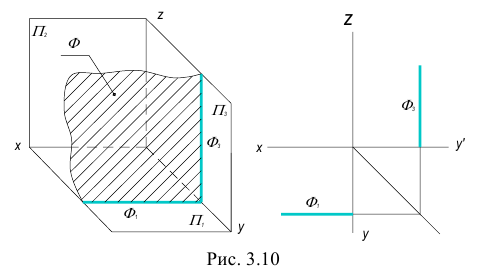
3. Профильная плоскость – плоскость, параллельная профильной плоскости проекций.

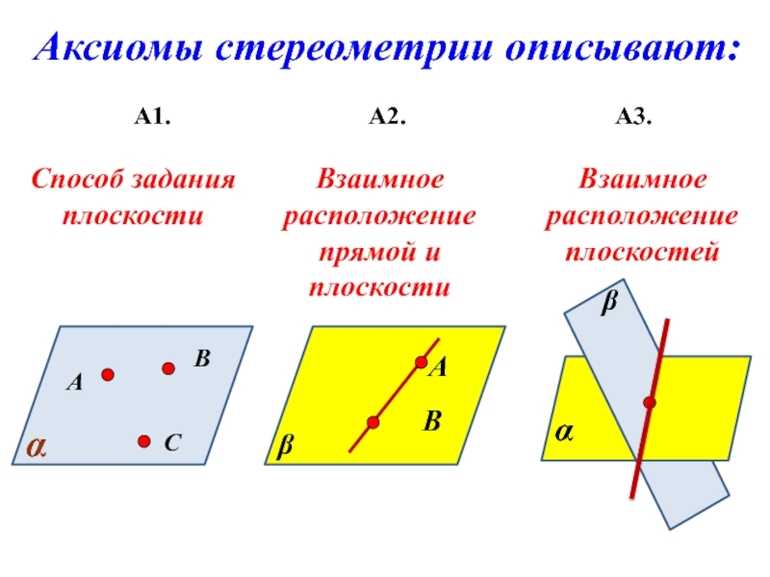
Взаимное расположение плоскостей

Если исследовать несколько двумерных геометрических объектов в пространстве, то их можно расположить несколькими различными способами относительно друг друга. Существует в общем случае всего два принципиально отличающихся варианта:

наличие пересечения;
отсутствие пересечения.

Каждый из этих случаев взаимного расположения плоскостей требует отдельного рассмотрения. Любопытно заметить, что, в отличие от прямых в пространстве, не существует накрест лежащих двумерных объектов. Если они не пересекаются, значит, являются параллельными, и наоборот.

Изучение пересечения

Для математического рассмотрения пересечения двух плоскостей удобно воспользоваться уравнением общего типа, поскольку оно в явной форме содержит координаты нормального вектора. Пусть заданы следующие две плоскости:

A1*x + B1*y + C1*z + D1 = 0;
A2*x + B2*y + C2*z + D2 = 0.

Очевидно, что они будут пересекаться тогда и только тогда, когда угол между их нормалями будет отличен от нуля. Рассчитать его можно, если воспользоваться свойством скалярного произведения векторов n1- и n2-. Искомая формула имеет следующий вид:

θ = arccos (|(A1*A2 + B1*B2 + C1*C2)|/((A1 2 +B1 2 + C1 2 )^0,5* (A2 2 +B2 2 + C2 2 )^0,5)).

Следует обратить внимание, что в числителе выражения стоит знак модуля по причине того, что угол между пересекающимися плоскостями всегда является острым.

Под каким бы углом ни пересекались две плоскости, происходит это строго по прямой линии. Ее уравнение можно найти, если решить систему из двух общих выражений для рассматриваемых объектов. При этом направляющий вектор прямой, по которой плоскости пересекаются, определяется как векторное произведение нормалей n1- и n2-. Очевидно, что расстояние между рассматриваемыми плоскостями всегда равно нулю, независимо от угла их пересечения.

Вопрос параллельности

Если две плоскости не пересекаются, то они всегда будут параллельными друг другу. При решении геометрических задач для доказательства параллельности можно применить один из следующих способов:

Первый: найти векторное произведение нормалей обоих объектов. Если получится нулевой результат, значит, они являются параллельными.
Второй: представить один нормальный вектор в виде умножения второго на некоторое число (если делить одну нормаль на другую покоординатно, то получится конкретное числовое значение). Если удается выполнить эту операцию, то оба вектора являются параллельными, а значит, таковыми будут и задаваемые ими плоскости.
Третий: вычислить угол между нормалями, используя свойства скалярного произведения. Если получится 0°, то рассматриваемые объекты являются параллельными.

Помимо этих трех способов, существует также признак параллельности плоскостей. Соответствующую теорему можно сформулировать следующим образом: если каждая из двух пересекающихся прямых одной плоскости параллельна соответствующей прямой для другой плоскости, то рассматриваемые двумерные объекты не имеют общих точек.

Для доказательства этого утверждения необходимо воспользоваться кратко свойством транзитивности: пара пересекающихся прямых однозначно задает нормаль плоскости. Поскольку они попарно параллельны, то нормали также будут параллельны друг другу.

Важным свойством параллельных плоскостей является тот факт, что пересекающие их две прямые, которые параллельны друг другу, отсекают на них отрезки одинаковой длины.

Между двумя непересекающимися двумерными объектами существует определенное расстояние, которое всегда отлично от нуля. Это утверждение следует из определения параллельных плоскостей. Вычислить его можно с помощью следующей формулы:

d = |A1*x0 + B1*y0 + C1*z0 + D1|/(A1 2 + B1 2 + C1 2 )^0,5.

Здесь (x0, y0, z0) — принадлежащая второй плоскости точка.

Чем можно заменить слово «взаимно»?

Если вы пишите текст или сочинение про взаимность, то вам понадобятся синонимы или слова близкие по смыслу. Чем можно заменить слово «взаимно»?

В качестве альтернативы часто используются такие слова, выражения и формулировки:

«Аналогично»
«Я тебя тоже»
«И я»
«Твои чувства обоюдные»
«Я разделяю твои чувства»
«Я тоже к тебе хорошо отношусь»
«Ты мне тоже симпатичен»
«Мы с тобой думаем одинаково»
«Я согласен» и т.д.

Зачастую многие влюбленные обижаются на слово «взаимно». Поскольку считают это слишком сдержанным и коротким ответом. Действительно, ответ «Взаимно» на фразу «Я тебя люблю» звучит так, как будто партнер пока еще не уверен в полноте своих чувств, стесняется, или не хочет говорить слово «люблю» и т.д.

Способы задания прямой в пространстве.

Существует несколько способов, позволяющих однозначно определить прямую линию в пространстве. Перечислим основные из них.

Мы знаем из аксиомы, что через две точки проходит прямая, причем только одна. Таким образом, если мы отметим две точки в пространстве, то это позволит однозначно определить прямую линию, проходящую через них.

Если в трехмерном пространстве введена прямоугольная система координат и задана прямая с помощью указания координат двух ее точек, то мы имеем возможность составить уравнение прямой, проходящей через две заданные точки.

Второй способ задания прямой в пространстве основан на теореме: через любую точку пространства, не лежащую на данной прямой, проходит прямая, параллельная данной, и причем только одна.

Таким образом, если задать прямую (или отрезок этой прямой) и не лежащую на ней точку, то мы однозначно определим прямую, параллельную заданной и проходящей через данную точку.

Рекомендуем также ознакомиться со статьей уравнение прямой, проходящей через заданную точку параллельно заданной прямой.

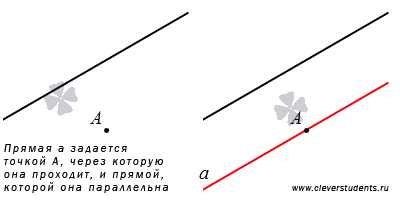
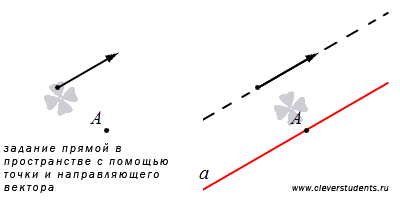
Можно указать точку, через которую проходит прямая и ее направляющий вектор. Это также позволит однозначно определить прямую.

Если прямая задана таким способом относительно зафиксированной прямоугольной системы координат, то мы можем сразу записать ее канонические уравнения прямой в пространстве и параметрические уравнения прямой в пространстве.

Следующий способ задания прямой в пространстве основан на аксиоме стереометрии: если две плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей.

Таким образом, задав две пересекающиеся плоскости, мы однозначно определим прямую в пространстве.

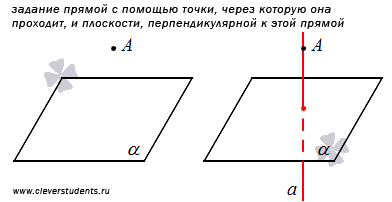
Еще один способ задания прямой в пространстве следует из теоремы (ее доказательство Вы можете найти в книгах, указанных в конце этой статьи): если задана плоскость и не лежащая в ней точка, то существует единственная прямая, проходящая через эту точку и перпендикулярная к заданной плоскости.

Таким образом, чтобы определить прямую, можно задать плоскость, которой искомая прямая перпендикулярна, и точку, через которую эта прямая проходит.

Если прямая задана таким способом относительно введенной прямоугольной системы координат, то будет полезно владеть материалом статьи уравнения прямой, проходящей через заданную точку перпендикулярно к заданной плоскости.

Список литературы.

Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б., Позняк Э.Г., Юдина И.И. Геометрия. 7 – 9 классы: учебник для общеобразовательных учреждений.
Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б., Киселева Л.С., Позняк Э.Г. Геометрия. Учебник для 10-11 классов средней школы.
Бугров Я.С., Никольский С.М. Высшая математика. Том первый: элементы линейной алгебры и аналитической геометрии.
Ильин В.А., Позняк Э.Г. Аналитическая геометрия.

Некогда разбираться?

Решение задачи

Заданы две плоскости в пространстве следующими уравнениями:

x + 2*y — z = 0 и

(x, y, z) = (-1,5, 0,) + α*(-2, 1, 0) + β*(1, 0, 1).

Необходимо доказать, что оба объекта являются параллельными.

Для решения этой задачи нельзя сразу воспользоваться одним из трех способов доказательства параллельности, поскольку векторное уравнение не содержит в явной форме нормальный вектор. Чтобы его получить, необходимо векторно умножить два направляющих отрезка этой плоскости:

= (1, 2, -1).

В свою очередь, нормаль первой плоскости имеет координаты (1, 2, -1), то есть она совпадает с нормалью для второй плоскости. Это означает, что оба двумерных объекта являются параллельными.

Таким образом, плоскости в пространстве могут либо пересекаться, либо быть параллельными. Для выполнения условия параллельности необходимо и достаточно, чтобы их нормали не пересекались, то есть угол между ними составлял 0°.

Примеры употребления слова «взаимно»

Иногда бывает так, что слово «взаимно» используется в качестве ответа на пожелания. К примеру, — «желаю долгой и счастливой жизни», — «взаимно». Где еще употребляется такая словоформа? Вот примеры:

Привет, Сережа! От всей души поздравляю тебя с Днем Программиста! Желаю, чтобы все у тебя было и тебе за это ничего не было! – Спасибо, коллега! Взаимно!
С праздниками! Маме привет! – Спасибо, взаимно!
Знаешь, ты мне очень нравишься… — Все взаимно (кстати, «все взаимно» в данном случае, более обнадеживающий вариант

Особенно, если он сказан игривым и оптимистичным тоном).
Чтоб вам пусто было! Опять затопили мою квартиру – Спасибо, Галина Дмитриевна! Взаимно!
Раньше было «хорошо», а теперь – «взаимно».
Вова, как же ты меня бесишь! – Не волнуйся, дружище, это взаимно!
Я любил тебя давно, но не знал, что это взаимно.
Важно, чтобы все было взаимно. А возраст, рост, вес, раса и цвет кожи для любви не имеют значения.
У вас, гляжу, все взаимно! – Ну, как видишь!
Тебе привет от Тиграна! Желает счастья в личной жизни! – Передай ему, что это взаимно!
Я прямо не знаю, что тебе сказать «я тебя люблю» или «взаимно»

– А чего тут думать, милый? Скажи: «выходи за меня замуж».

Попробуйте самостоятельно составить предложения. Благодаря этому вы лучше поймете материал и сможете понять всю суть данного слова. Ниже еще больше примеров. Читайте далее.

«Взаимно», «не взаимно»: что означают слова?

«Взаимно», «не взаимно»

Множество вещей в мире делается именно «по взаимному согласию». Даже если дело касается бизнеса, параллельно с «выгодностью» сделки также рассматривается и надежность партнеров. И выбор всегда останавливается на тех, к кому имеется доверие и личная симпатия. Что означает слово «взаимно» и «не взаимно»?

Основная сфера понятий «взаимность» и «невзаимость», все же, любовная. Здесь наличие обоюдного чувства важнее всего. Ведь если влюбленность либо же просто интерес чувствует кто-то один, а второй, в свою очередь, считает, что ему это не нужно – то эта любовь ни к чему не приведет.
В свою очередь, отсутствие взаимности – это ситуация, когда у одного человека чувства есть, а у другого – нет. Конечно же, никто не обязан любить по принуждению. Но отказ может быть бесцеремонным и грубым, а может быть – вежливым и тактичным. В последнем случае, объект симпатии будет чист с моральной точки зрения.

Осознавать отсутствие взаимности всегда болезненно. В то время как ее наличие может заставить человека трепетать от счастья.

Полуплоскости. Сонаправленные лучи

Любая прямая делит плоскость на две полуплоскости.

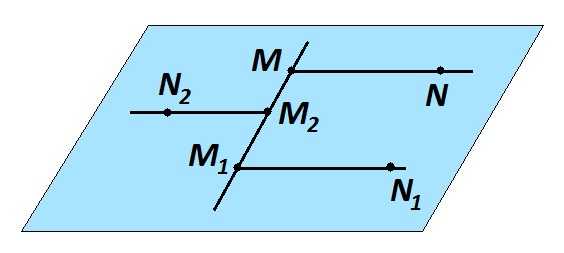
Лучи называют сонаправленными, если они лежат в одной полуплоскости и параллельны.

Параллельные и лежащие в разных полуплоскостях лучи не являются сонаправленными. На рисунке лучи MN и \(M_1N_1 \)— сонаправленные, а MN и \(M_2N_2, M_1N_1\) и \(M_2N_2\) — параллельны, но не сонаправлены.

Теорема 4

Два угла равны, если две их стороны соответственно сонаправлены.

Доказательство:

Приведем доказательство для углов, лежащих в разных плоскостях. Изобразим ∠А и \(∠А_1 \)на чертеже.

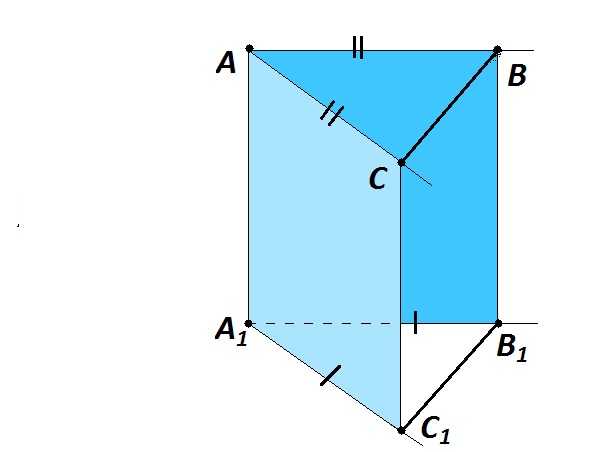
Сонаправленные лучи параллельны ⇒ соответственно параллельны стороны углов. Так как через параллельные прямые можно провести единственную плоскость, проведем через них две плоскости. На сторонах угла А и угла А1 отметим точки С, В и С1, В1 соответственно — так, чтобы \(АС=А_1С_1\) и \(АВ=А_1В_1\). Получившаяся объемная фигура имеет вид треугольной призмы.
У полученного четырехугольника \(AВВ_1A_1\) противолежащие стороны AВ и \(A_1В_1\) равны и параллельны по условию. Это значит, что \(AВВ_1A_1\) — параллелограмм. \(AA_1 =ВВ_1, AA_1||ВВ_1\).
Аналогично выясним, что \(AСС_1A_1\) — параллелограмм, и \(СС_1=АА_1, СС_1||АА_1\).
\(СС_1\) и \(BB_1\) равны и параллельны третьему отрезку \(АА_1\), следовательно: они равны и параллельны между собой, т. е. \(СС_1||BB_1\) и \(СС_1= BB_1\). Значит \(ВСС_1В_1\) — параллелограмм, и из этого получаем: \(ВС=В_1С_1\).
Так как \(АВ=А_1В_1, AС =A_1С_1\) и \(СB=С_1B_1\), выясняем, что ΔABС и \(ΔA_1B_1С_1\) равны по трем сторонам, и поэтому \(А=А_1.\)

Теоремы взаимного расположения прямой и окружности

1. Касательная к окружности перпендикулярна радиусу, проведенному к точке касания.

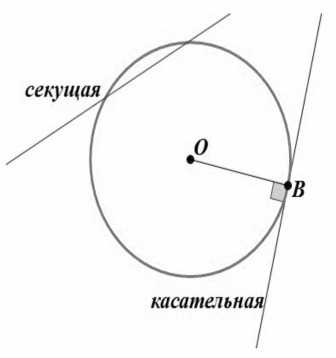
Рисунок 4

2. Если из данной точки проведены к окружности две касательные, то отрезки касательных равны между собой и центр окружности лежит на биссектрисе угла с вершиной в этой точке: AB = AC.

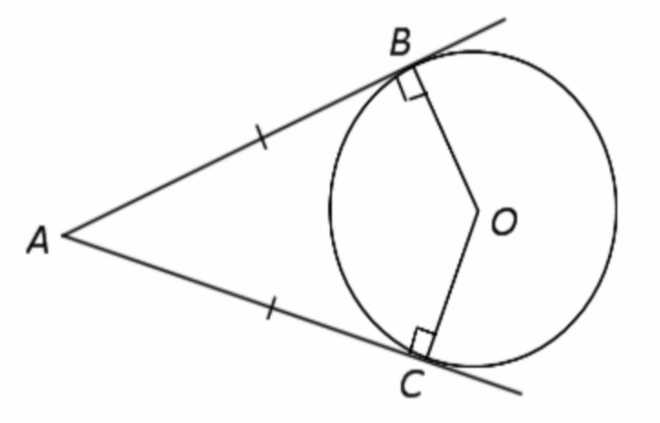
Рисунок 5

3. Если из данной точки проведены к окружности касательная и секущая, то квадрат длины отрезка касательной равен произведению всего отрезка секущей на его внешнюю часть: AC2 = CD×BC.

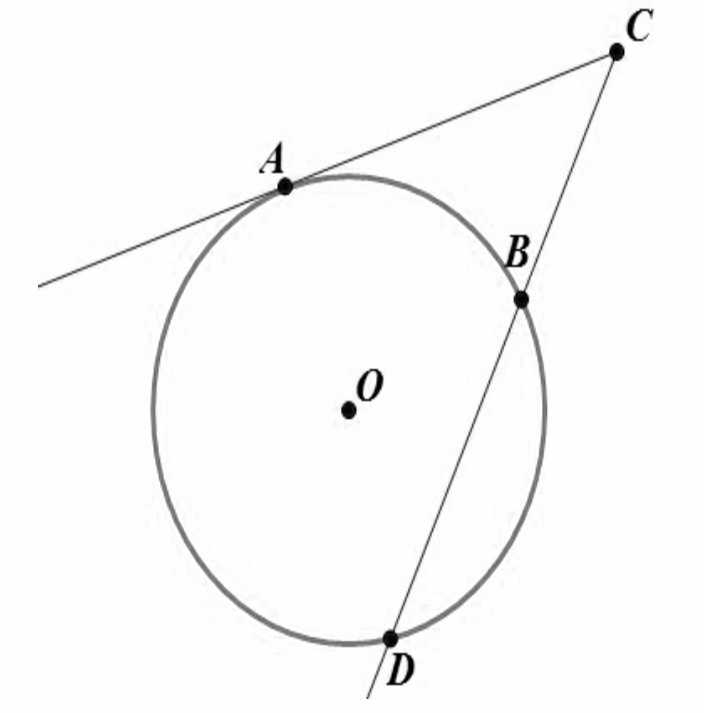
Рисунок 6

4. Произведение всего отрезка одной секущей на его внешнюю часть равно произведению всего отрезка другой секущей на его внешнюю часть: AC×BC = EC×DC.

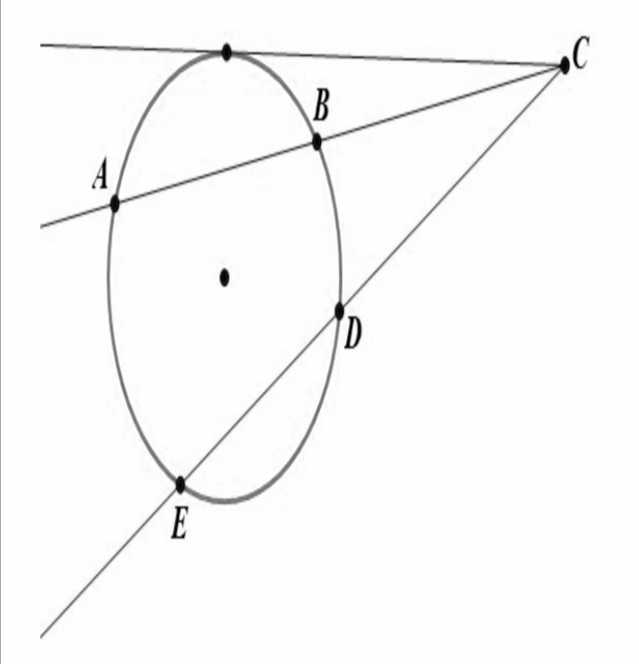
Рисунок 7

Что значит, если «взаимно» говорит парень?

«Взаимно»

Некоторые представительницы прекрасного пола теряются, когда слышат от мужчины слово «взаимно». Почему так происходит? Что значит, если «взаимно» говорит парень?

С одной стороны, оно говорит о том, что девушка ему интересна.
Но с другой стороны, короткий ответ подразумевает и апатию, полное отсутствие рвения.
Соответственно, сказав девушке «взаимно», парень не побежит к ней «на крыльях любви», не станет писать стихи либо рвать цветы с ближайшей клумбы. Скорее всего, через секунду он забудет об этой девушке и будет играть в свою любимую компьютерную игру.

Получается, что мужской ответ «взаимно» — это скрытое «нет». То есть, человек не разделяет чувства, но не хочет обижать собеседника. Таким образом, парень хочет, чтобы девушка услышала то, что она хочет услышать, и наконец, оставила его в покое. На самом же деле, чувств, в таком случае, может и не быть.

Однако стоит помнить, что парни вообще немногословные существа. Поэтому он может говорить «взаимно» и если действительно любит. Варианты: слишком стеснительный и боится, что слово «люблю» наложит на него какие-то обязательства, в данный момент занят (потому пишет кратко) и т.д.

Часто парни не предают слову «взаимно» негативный оттенок. Поэтому, они совершенно не понимают, почему девушки обижаются на этот ответ. Допустим, если парень скажет парню «ты мне друг! – Взаимно», никто из них и не подумает, что кто-то скуп на проявление взаимности, что кто-то обижен, что кто-то лукавит и врет и т.д.

Некоторым парням достаточно более простого проявления любви и дружбы в стиле: «Ты мне друг? – Да, конечно!», «Ты меня любишь?– Ага».

В то время как девушки наделяют слова более многогранными смыслами. В их понимании, написал только лишь «взаимно» — значит, не любит. А вот если бы написал полностью «Я люблю тебя», и при этом добавил бы «больше жизни», «схожу с ума от любви к тебе» и прочие «эпитеты» — то тогда взаимность получена в полной мере.

Мужская скупость на слова впитывается многими парнями с молоком матери. Считается, что мужчина должен не говорить, а только делать. Именно поэтому «взаимно» для некоторых – вполне нормальный ответ. Если можно ответить так на комплимент коллеги по футбольной команде или на похвалу другого (равного) участника коллектива, то почему нельзя сказать так девушке?

Двумерный объект в пространстве

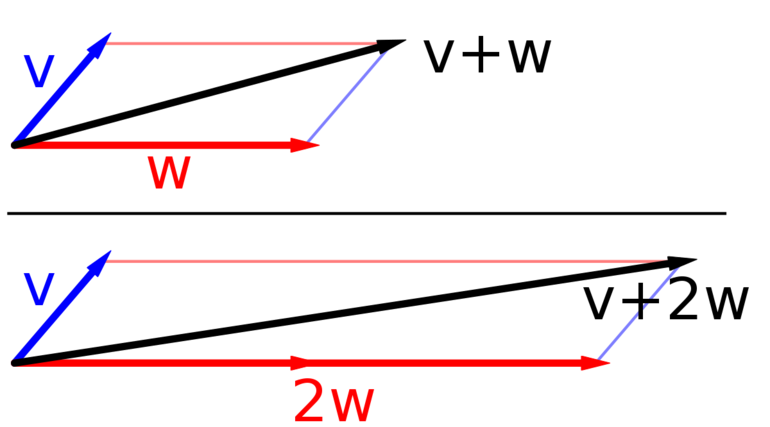
Именно таковым является любая плоскость. Чтобы понять, как она задается, следует рассмотреть два произвольных вектора, которые не лежат на одной прямой. Сумма этих векторов, каждый из которых умножается на произвольное число, задает бесконечный набор точек в пространстве. Совокупность последних однозначно определяет изучаемый объект. Этот способ построения интуитивно понятен. Математически можно записать:

(x, y, z) = (x0, y0, z0) + α *u- + β*v-.

Здесь u- и v- — это задающие плоскость векторы, α и β — произвольные рациональные числа, которые удлиняют или укорачивают исходные направленные отрезки, (x0, y0, z0) — координаты конкретной точки в пространстве, которая однозначно определяет двумерный объект из всего их параллельного набора. Любые x, y, z, которые удовлетворяют этому выражению, относятся к рассматриваемой плоскости.

Необходимо отчетливо понимать, что изучаемый геометрический объект имеет смысл рассматривать только в трехмерном пространстве, поскольку сам он является двумерным. Например, рабочая тетрадь школьников сама по себе представляет собой единственный двумерный объект.

Нормальный вектор

Направленный отрезок, который пересекает изучаемый геометрический объект под прямым углом, называется нормальным. Соответственно, прямая, параллельная нормальному вектору, будет нормалью. Этот отрезок очень важен для понимания свойств плоскостей параллельных и пересекающихся. Кроме того, с его помощью удобно задавать сам рассматриваемый геометрический объект, при этом получается уравнение общего типа.

Если известны координаты нормали, то автоматически становится понятным, какие параллельные плоскости он задает. Их бесконечное количество. Для определения единственного объекта необходимо зафиксировать точку в пространстве, например, P0 (x0, y0, z0). Пусть P (x, y, z) также принадлежит плоскому объекту, тогда векторы PP0- и n- являются перпендикулярными, где n-(A, B, C) — нормаль. Так как следствием перпендикулярности направленных отрезков является равенство нулю их скалярного произведения, то можно записать следующее равенство:

(PP0-*n-) = 0.

Подставляя в него известные координаты и упрощая математическое выражение, получают следующее уравнение:

A*x + B*y + C*z + D = 0, где D = -A*x0 — B*y0 — C*z0.

Это выражение называется явным, или общего типа. Оно содержит в себе координаты нормального вектора, поэтому им легко пользоваться при решении геометрических задач.

Математические представления

Существует несколько вариантов записи уравнений изучаемого двумерного объекта. Каждым из них удобно пользоваться при решении того или иного типа задач. Основными уравнениями являются следующие:

Векторное. Соответствующее ему выражение имеет вид: (x, y, z) = (x0, y0, z0) + α *u- + β*v-.
Общего типа, или явное. Его математическое выражение A*x + B*y + C*z + D = 0, где нормалью является вектор n-(A, B, C).
Параметрическое. Оно получается, если в явном виде переписать векторное представление: x = x0 + α*ux + β*vx; y = y0 + α*uy + β*vy; z = z0 + α*uz + β*vz. Здесь u (ux, uy, uz) и v (vx, vy, vz). Параметры α и β могут принимать произвольные и независимые друг от друга значения.
В отрезках. Математическая запись этого типа представления выглядит так: x/p + y/q + z/r = 1, где p, q, r — некоторые положительные или отрицательные числа. Если двумерный объект имеет представление в отрезках, то легко нарисовать его наглядное изображение на координатной плоскости, поскольку он отсекает на осях x, y и z отрезки p, q и r соответственно. Для доказательства этого утверждения достаточно положить равными нулю две координаты, например, x и z, а затем выразить из равенства третью.

На первый взгляд, четыре типа математических представлений рассматриваемого объекта могут показаться независимыми, однако это не так. Каждое представление с помощью несложных математических преобразований может быть переведено в любое другое.

Например, чтобы из явного представления получить векторное, необходимо сначала выразить какую-либо переменную из него. Затем представить через полученное выражение произвольную точку плоскости (x, y, z). После этого следует разложить правую часть равенства на три вектора, разделяя неизвестные переменные. Векторная форма получается путем вынесения за скобки двух неизвестных переменных и их последующей замены на параметры α и β.

https://youtube.com/watch?v=O1so8REgHlo

Пояснение на примерах

Пример 1

Точка А расположена вне окружности радиуса R и удалена от центра О этой окружности на расстояние d. Чему равно наименьшее расстояние от точки А до точек данной окружности?

Пусть В — точка пересечения окружности с от резком ОА. Покажем, что расстояние АВ является наименьшим из возможных от точки А до точек окружности. Действительно, для любой другой точки С окружности выполняется неравенство : АВ + ВO < АС + СO. Так как ВО = СО = R, получим АВ < АС. Учитывая, что АО = d, ВO = R, получаем, что искомое наименьшее расстояние равно длине отрезка АВ = d − R.

Пример 1
Пример 2

Из одной точки проведены две касательные к окружности. Докажите, что отрезки касательных, заключенные между этой точкой и точками касания, равны.

Рассмотрим две касательные к окружности с центром в точке О, проведенные из точки А, и касающиеся окружности в точках В и С. Треугольники АОВ и АОС — прямоугольные, ОВ = ОС, сторона АО — общая. По признаку равенства прямоугольных треугольников они равны. Следовательно, АВ = АС.

Угол между скрещивающимися прямыми

Углом между скрещивающимися прямыми называют угол между, соответственно данным (рис. 2).

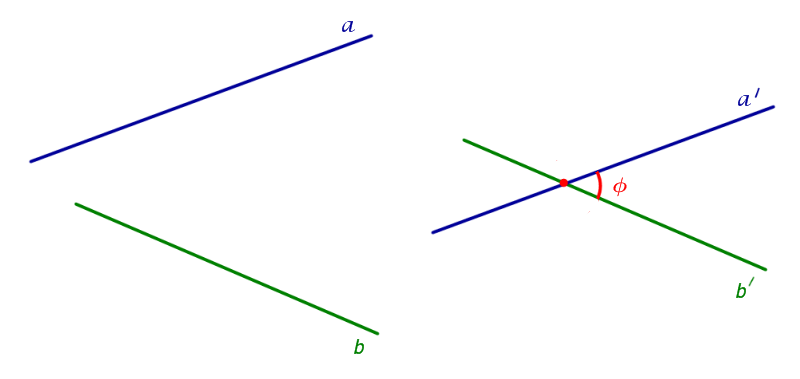
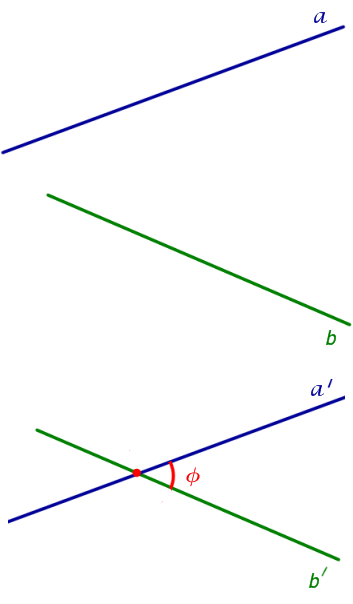
Рис.2

На рисунке 2 изображены скрещивающиеся прямые a и b. Прямая a’ параллельна прямой a, прямая b’ параллельна прямой b. Прямые a’ и b’ пересекаются. Угол φ и является углом между скрещивающимися прямыми a и b.

Задача. В ABCDA₁B₁C₁D₁ найти угол между прямыми AB₁ и BC₁.

Решение. Поскольку прямая AB₁ пересекает плоскость BB₁C₁ в точке B₁, которая не лежит на прямой BC₁, то прямые AB₁ и BC₁ скрещиваются (рис. 3).

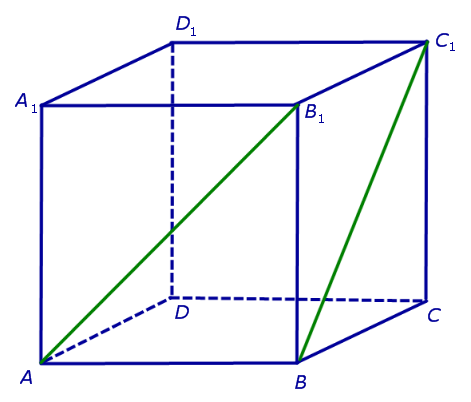
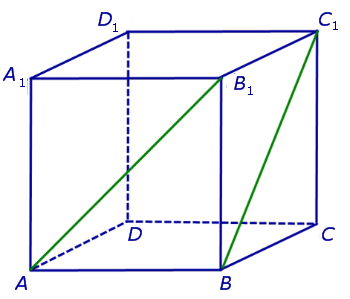
Рис.3

Для того, чтобы найти угол между прямыми AB₁ и BC₁, проведем в кубе диагональ AD₁ и диагональ верхнего D₁B₁ (рис. 4).

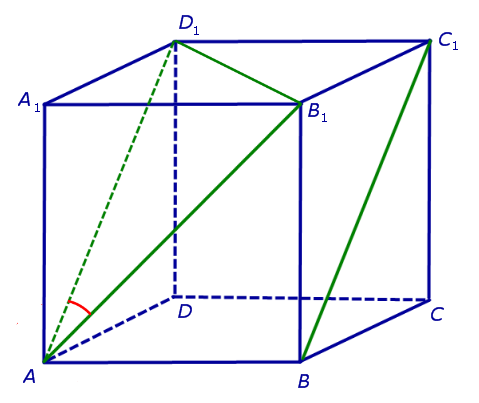
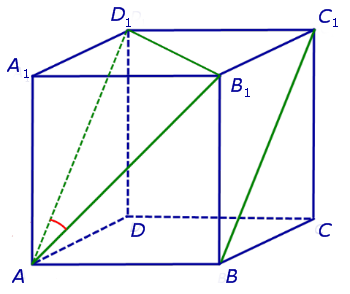
Рис.4

По определению угол D₁AB₁ и является углом между прямыми AB₁ и BC₁. Поскольку треугольник AD₁B₁ , угол D₁AB₁ равен 60°.

Ответ. 60°.

На сайте можно также ознакомиться с нашими учебными материалами для подготовки к ЕГЭ по математике.

Взаимное расположение прямых в пространстве

Две прямые пространства могут:

1) скрещиваться;

2) пересекаться в точке ;

3) быть параллельными ;

4) совпадать.

Случай № 1 принципиально отличается от других случаев. Две прямые скрещиваются, если они не лежат в одной плоскости. Поднимите одну руку вверх, а другую руку вытяните вперёд – вот вам и пример скрещивающихся прямых. В пунктах же № 2-4 прямые обязательно лежат в одной плоскости.

Как выяснить взаимное расположение прямых в пространстве?

Рассмотрим две прямые пространства:

– прямую , заданную точкой и направляющим вектором ;
– прямую , заданную точкой и направляющим вектором .

Для лучшего понимания выполним схематический чертёж: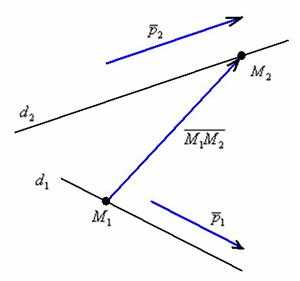
На чертеже в качестве примера изображены скрещивающиеся прямые.

Как разобраться с этими прямыми?

Так как известны точки , то легко найти вектор .

Если прямые скрещиваются, то векторы не компланарны (см. урок Линейная (не) зависимость векторов. Базис векторов), а, значит, определитель, составленный из их координат, ненулевой. Или, что фактически то же самое, смешанное произведение векторов будет отлично от нуля: .

В случаях № 2-4 наша конструкция «падает» в одну плоскость, при этом векторы компланарны, а смешанное произведение линейно зависимых векторов равняется нулю: .

Раскручиваем алгоритм дальше. Предположим, что , следовательно, прямые либо пересекаются, либо параллельны, либо совпадают.

Если направляющие векторы не коллинеарны, то прямые пересекаются. Как проверить два вектора на коллинеарность, подробно рассмотрено в той же статье Линейная (не) зависимость векторов. Базис векторов.

Если направляющие векторы коллинеарны, то прямые либо параллельны, либо совпадают. Финальным гвоздём предлагаю следующий приём: берём какую-либо точку одной прямой и подставляем её координаты в уравнение второй прямой; если координаты «подошли», то прямые совпадают, если «не подошли», то прямые параллельны.

Ход алгоритма незатейлив, но практические примеры всё равно не помешают:

Пример 11

Выяснить взаимное расположение двух прямых

Решение: как и во многих задачах геометрии, решение удобно оформить по пунктам:

1) Вытаскиваем из уравнений точки и направляющие векторы:

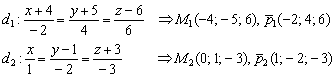
2) Найдём вектор:

3) Вычислим смешанное произведение векторов:

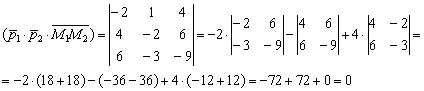
Таким образом, векторы компланарны, а значит, прямые лежат в одной плоскости и могут пересекаться, быть параллельными или совпадать.

4) Проверим направляющие векторы на коллинеарность.

Составим систему из соответствующих координат данных векторов:

Из каждого уравнения следует, что , следовательно, система совместна, соответствующие координаты векторов пропорциональны, и векторы коллинеарны.

Вывод: прямые параллельны либо совпадают.

5) Выясним, есть ли у прямых общие точки. Возьмём точку , принадлежащую первой прямой, и подставим её координаты в уравнения прямой :

Таким образом, общих точек у прямых нет, и им ничего не остаётся, как быть параллельными.

Ответ:

Интересный пример для самостоятельного решения:

Пример 12

Выяснить взаимное расположение прямых

Обратите внимание, что у второй прямой в качестве параметра выступает буква. Логично

В общем случае – это же две различные прямые, поэтому у каждой прямой свой параметр.

И снова призываю не пропускать примеры, ~~пороть буду~~ предлагаемые мной задачи далеко не случайны

Взаимное расположение прямой и точки.

Начать следует с аксиомы: на каждой прямой и в каждой плоскости имеются точки.

Точки принято обозначать большими латинскими буквами, например, точки А и F. В свою очередь прямые линии обозначают малыми латинскими буквами, к примеру, прямые a и d.

Возможны два варианта взаимного расположения прямой и точки на плоскости: либо точка лежит на прямой (в этом случае также говорят, что прямая проходит через точку), либо точка не лежит на прямой (также говорят, что точка не принадлежит прямой или прямая не проходит через точку).

Для обозначения принадлежности точки некоторой прямой используют символ «». К примеру, если точка А лежит на прямой а, то можно записать . Если точка А не принадлежит прямой а, то записывают .

Справедливо следующее утверждение: через любые две точки проходит единственная прямая.

Это утверждение является аксиомой и его следует принять как факт. К тому же, это достаточно очевидно: отмечаем две точки на бумаге, прикладываем к ним линейку и проводим прямую линию. Прямую, проходящую через две заданные точки (например, через точки А и В), можно обозначать двумя этими буквами (в нашем случае прямая АВ или ВА).

Следует понимать, что на прямой, заданной на плоскости, лежит бесконечно много различных точек, причем все эти точки лежат в одной плоскости. Это утверждение устанавливается аксиомой: если две точки прямой лежат в некоторой плоскости, то все точки этой прямой лежат в этой плоскости.

Множество всех точек, расположенных между двумя заданными на прямой точками, вместе с этими точками называют отрезком прямой или просто отрезком. Точки, ограничивающие отрезок, называются концами отрезка. Отрезок обозначают двумя буквами, соответствующими точкам концов отрезка. К примеру, пусть точки А и В являются концами отрезка, тогда этот отрезок можно обозначить АВ или ВА

Обратите внимание, что такое обозначение отрезка совпадает с обозначением прямой. Чтобы избежать путаницы, рекомендуем к обозначению добавлять слово «отрезок» или «прямая».

Для краткой записи принадлежности и не принадлежности некоторой точки некоторому отрезку используют все те же символы и . Чтобы показать, что некоторый отрезок лежит или не лежит на прямой пользуются символами и соответственно. К примеру, если отрезок АВ принадлежит прямой а, можно кратко записать .

Следует также остановиться на случае, когда три различных точки принадлежат одной прямой. В этом случае одна, и только одна точка, лежит между двумя другими. Это утверждение является очередной аксиомой. Пусть точки А, В и С лежат на одной прямой, причем точка В лежит между точками А и С. Тогда можно говорить, что точки А и С находятся по разные стороны от точки В. Также можно сказать, что точки В и С лежат по одну сторону то точки А, а точки А и В лежат по одну сторону от точки С.

Для полноты картины заметим, что любая точка прямой делит эту прямую на две части – два луча. Для этого случая дается аксиома: произвольная точка О, принадлежащая прямой, делит эту прямую на два луча, причем две любые точки одного луча лежат по одну сторону от точки О, а две любые точки разных лучей – по разные стороны от точки О.

Задачи с прямой в пространстве

В заключительной части урока я постараюсь рассмотреть максимальное количество различных задач с пространственными прямыми. При этом будет соблюдён начатый порядок повествования: сначала мы рассмотрим задачи со скрещивающимися прямыми, затем с пересекающимися прямыми, и в конце поговорим о параллельных прямых в пространстве. Однако должен сказать, что некоторые задачи данного урока можно сформулировать сразу для нескольких случаев расположения прямых, и в этой связи разбиение раздела на параграфы несколько условно. Есть более простые примеры, есть более сложные примеры, и, надеюсь, каждый найдёт то, что нужно.

Взаимное расположение прямой и точки

Имеем аксиому:

Определение 1

На каждой прямой и в каждой плоскости могут быть отмечены точки.

Точки обозначают как большими, так и маленькими латинскими буквами. Например, А и D или a и d.

Для точки и прямой известны только два варианта расположения: точка на прямой, иначе говоря, что прямая проходит через нее, или точка не на прямой, то есть прямая не проходит через нее.

Чтобы обозначить, принадлежит точка плоскости или точка прямой, используют знак «∈». Если в условии дано, что точка A лежит на прямой a, тогда это имеет такую форму записи A∈a. В случае, когда точка А не принадлежит, тогда другая запись A∉a.

Справедливо суждение:

Определение 2

Через любые две точки, находящиеся в любых плоскостях, существует единственная прямая, которая проходит через них.

Данное высказывание считается акисомой, поэтому не требует доказательств. Если рассмотреть это самостоятельно, видно, что при существующих двух точках имеется только один вариант их соединения. Если имеем две заданные точки А и В, то прямую, проходящую через них можно назвать данными буквами, например, прямая АВ. Рассмотрим рисунок, приведенный ниже.

Прямая, расположенная на плоскости, имеет большое количество точек. Отсюда исходит аксиома:

Определение 3

Если две точки прямой лежат в плоскости, то и все остальные точки данной прямой принадлежат плоскости.

Множество точек, находящееся между двумя заданными, называют отрезком прямой. Он имеет начало и конец. Введено обозначение двумя буквами.

Если дано, что точки А и Р – концы отрезка, значит, его обозначение примет вид РА или АР. Так как обозначения отрезка и прямой совпадают, рекомендовано дописывать или договаривать слова «отрезок», «прямая».

Краткая запись принадлежности включает в себя использование знаков ∈ и ∉. Для того, чтобы зафиксировать расположение отрезка относительно заданной прямой, применяют ⊂. Если в условии дано, что отрезок АР принадлежит прямой b, значит, и запись будет выглядеть следующим образом: АР⊂b.

Случай принадлежности одновременно трех точек одной прямой имеет место быть. Это верно, когда одна точка лежит между двумя другими. Данное утверждение принято считать аксиомой. Если даны точки А, В, С, которые принадлежат одной прямой, а точка В лежит между А и С, следует, что все заданные точки лежат на одной прямой, так как лежат по обе стороны относительно точки B .

Точка делит прямую на две части, называемые лучами.Имеем аксиому:

Определение 4

Любая точка O, находящаяся на прямой, делит ее на два луча, причем две любые точки одного луча лежат по одну сторону луча относительно точки O, а другие – по другую сторону луча.